 Figure 1
Figure 1Abstract
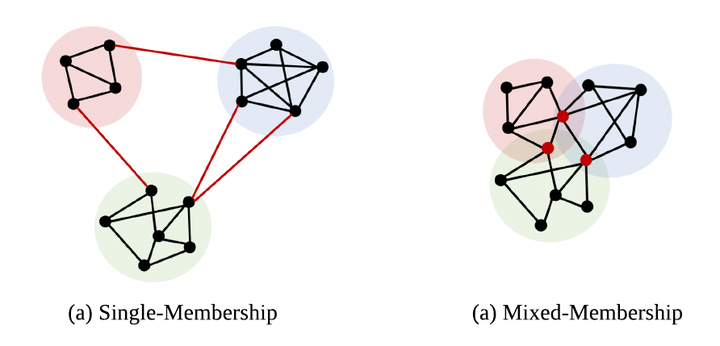
Unsupervised node clustering (or community detection) is a classical graph learning task. In this paper, we study algorithms, which exploit the geometry of the graph to identify densely connected substructures, which form clusters or communities. Our method implements discrete Ricci curvatures and their associated geometric flows, under which the edge weights of the graph evolve to reveal its community structure. We consider several discrete curvature notions and analyze the utility of the resulting algorithms. In contrast to prior literature, we study not only single-membership community detection, where each node belongs to exactly one community, but also mixed-membership community detection, where communities may overlap. For the latter, we argue that it is beneficial to perform community detection on the line graph, i.e., the graph’s dual. We provide both theoretical and empirical evidence for the utility of our curvature-based clustering algorithms. In addition, we give several results on the relationship between the curvature of a graph and that of its dual, which enable the efficient implementation of our proposed mixed-membership community detection approach and which may be of independent interest for curvature-based network analysis.